Limit fungsi adalah sebuah konsep yang ada pada pelajaran matematika, limit biasanya digunakan untuk menerangkan suatu sifat dari suatu fungsi. Seperti halnya pada saat sebuah argumen hampir mendekati suatu titik tak terhingga atau juga sifat dari suatu barisan saat indeks hampir mendekati titik tak terhingga. Pada umumnya limit digunakan pada materi kalkulus dan juga cabang lain dari matematika yang berfungsi untuk mencari suatu turunan dan juga lanjutan.
DEFINISI LIMIT
Secara umum limit didefinisikan jika f adalah fungsi yang telah didefinisikan oleh suatu interval terbuka dan mengandung a (dengan adanya kemungkinan pengecualian pada titik a) dan juga L merupakan bilang real. Limit adalah suatu batas yang menggunakan konsep pendekatan fungsi. Jadi, bisa dibilang limit adalah nilai yang didekati fungsi saat suatu titik mendekati nilai tertentu.
Dengan menggunakan rumus matematika di atas maka kita bisa membuat nilai f(x) menjadi sedekat mungkin dengan nilai L dengan cara membuat nilai x menjadi dekat dengan a.
Hasil dari limit f(x) jika nilai x mendekati a, adalah L. Oleh karena itu perlu ingat bahwa kalimat tersebut juga tetap berlaku walaupun f(a) ≠ L. Atau bahkan fungsi di dalam f(x) sudah tidak perlu lagi didefinisikan dengan titik a.
SIFAT SIFAT LIMIT
Misalkan f(x), g(x) adalah fungsi yang mempunyai nilai limit pada x mendekati c, dengan k dan c adalah bilangan real serta n adalah bilangan positif, maka:SYARAT SUATU FUNGSI MEMPUNYAI LIMIT DI TITIK TERTENTU
Berikut deskripsi ada tidaknya limit suatu fungsi f (
x) untuk
x mendekati
c
Dari gambar grafik diatas
-gambar A: mempunyai limit kiri sama dengan limit kanan
-gambar B: tidak mempunyai limit karena limit kiri tidak sama dengan limit kanan
-gambar C: mempunyai limit karena limit kiri sama dengan limit kanan
-gambar D: tidak mempunyai limit karena limit kiri tidak sama dengan limit kanan
CONTOH 1


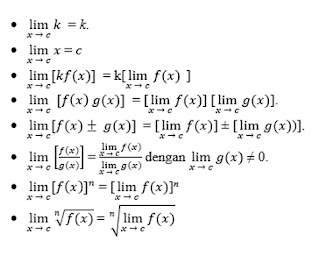




Komentar