FUNGSI,GRAFIK FUNGSI DAN OPERASI FUNGSI

APA ITU FUNGSI?

Menurut KBBI (Kamus Besar Bahasa Indonesia), fungsi dalam Matematika adalah besaran yang berhubungan. Jika besaran yang satu berubah, besaran yang lain juga berubah. 

Pengertian fungsi dalam matematika merupakan pemetaan setiap anggota sebuah himpunan (dinamakan sebagai domain), kepada anggota himpunan yang lain (dinamakan sebagai kodomain).

Jadi intinya, ada relasi atau hubungan gitu di antara kedua fungsi tersebut. 

Ada beberapa istilah penting di dalam fungsi matematika seperti domain (daerah asal fungsi f dilambangkan dengan D f), kodomain (daerah dari kawan fungsi f yang ditulis K f) dan range yang merupakan daerah hasil dilambangkan dengan R f.

perhatikan contoh fungsi dalam Matematika berikut ini:

• f(x)=2x+1 

bagaimana cara memetakan nilai A ke B-nya kalau ada fungsi f(x) = 2x + 1? 

pertama buat nilai A untuk disubstitusi dengan x. Kemudian, masukkan angkanya ke dalam fungsi f(x). 

Misal: A = 1, dengan begitu: 

• B = 2 (x) + 1
• B = 2(1) + 1 = 3, begitu seterusnya hingga seperti ini hasilnya:

 Nah, itulah yang disebut dengan fungsi matematika. Ini dia aturannya:

“Setiap anggota di A harus memiliki pasangan dengan tepat satu anggota di B”

Nah, dari ilustrasi di atas,kita bisa menuliskan nilai fungsi seperti berikut ini:

• f(x): A → B

Keterangan:

A: domain (daerah asal)

B: kodomain (daerah kawan)

SIFAT SIFAT FUNGSI

1.Fungsi Injektif 

Disebut fungsi satu-satu . Misalkan fungsi f menyatakan A ke B maka fungsi f disebut suatu fungsi satu-satu (injektif), apabila setiap dua elemen yang berlainan di A akan dipetakan pada dua elemen yang berbeda di B. Selanjutnya secara singkat dapat dikatakan bahwa f:A→B adalah fungsi injektif apabila a ≠ b berakibat f(a) ≠ f(b) atau ekuivalen, jika f(a) = f(b) maka akibatnya a = b.

2.Fungsi Surjektif 

Fungsi f: A → B disebut fungsi kepada atau fungsi surjektif jika dan hanya jika untuk sembarang b dalam kodomain B terdapat paling tidak satu a dalam domain A sehingga berlaku f ( a ) = b . Dengan kata lain, suatu kodomain fungsi surjektif sama dengan kisarannya ( range ). 

3.Fungsi Bijektif 

Suatu pemetaan f: A→B sedemikian rupa sehingga f merupakan fungsi yang injektif dan surjektif sekaligus, maka dikatakan “f adalah fungsi yang bijektif” atau “ A dan B berada dalam korespondensi satu-satu”.

Secara garis besar, fungsi terbagi atas fungsi aljabar dan fungsi transenden. Dari dua fungsi utama inilah kemudian muncul jenis fungsi lainnya, yaitu:

1. Fungsi Konstan

Fungsi yang terbentuk dari f(x)=k dengan k adalah konstanta atau saklar. Berapa pun nilai x yang disubtitusi maka nilainya selalu sama yaitu k.

2. Fungsi Identitas

Fungsi yang memetakan setiap anggota ke dirinya sendiri. Umumnya ditulis dengan f(x)=x. Grafik dari fungsi ini adalah garis yang nantinya membentuk sudut 45 derajat.

3. Fungsi Kuadrat

Fungsi yang berbentuk y = a2x² + a1x + a0. Grafik dari fungsi kuadrat berbentuk kurva parabola.

4. Fungsi Linear

Fungsi yang berbentuk f(x)=ax+b dengan a ≠ 0. Grafik dari fungsi ini berbentuk garis.

5. Fungsi Polinom

Merupakan bentuk umum dari fungsi konstan, linear, identitas dan kuadrat yang ditulis f(x) = an xn + an-1 xn-1 + … + a2x2 + a1x +a0

6. Fungsi Irasional

Fungsi ini berbentuk akar yang ditulis f(x) = √x+1

7. Fungsi Pecahan

Fungsi yang berbentuk pecahan.

8. Fungsi Ganjil

Fungsi yang memenuhi f(-x)==f(x). Untuk grafiknya yakni simetris terhadap titik pusat.

9. Fungsi Genap

Fungsi yang memenuhi f(-x)=f(x). Grafiknya simetris terhadap sumbu Y.

Untuk lebih memahami berikut ini contoh soalnya.

Jika f(x) = x² - 2 dan g(x) = 2x + 1 maka komposisi (f ο g)(x) adalah …

Jawaban:

f(x) = x² - 2

g(x) = 2x + 1

(f ο g)(x) = f( g(x) )

= f( 2x+1 )

= (2x+1)² - 2

= (4x²+4x+1) – 2

= 4x² + 4x – 1

Grafik Fungsi

Bilamana daerah asal dan daerah hasil sebuah fungsi merupakan bilangan riil, kita dapat membayangkan fungsi itu dengan menggambarkan grafiknya pada suatu bidang koordinat. Dan grafik fungsi $f$ adalah grafik dari persamaan $y=f\left(x\right)$. Gambar 1 berikut ini menampilkan grafik dari beberapa fungsi.

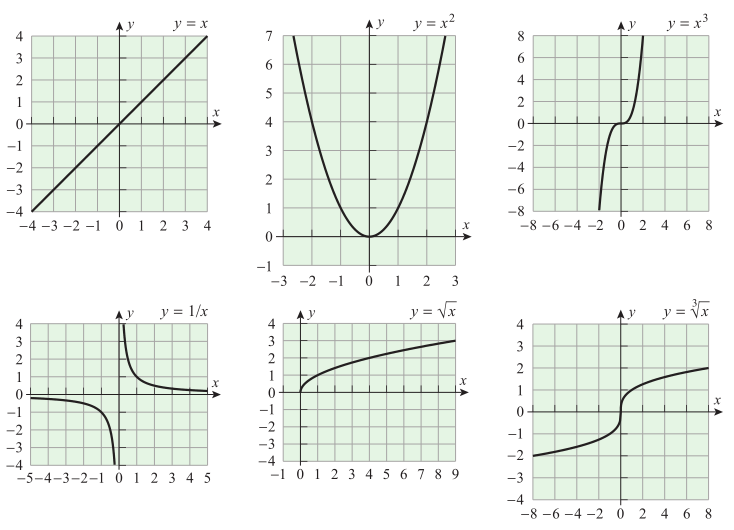
Gambar 1. Contoh grafik dari beberapa fungsi

OPERASI PADA FUNGSI

Fungsi bukanlah bilangan. Tetapi seperti halnya dua bilangan a dan b dapat ditambahkan untuk menghasilkan sebuah bilangan baru a + b, demikian juga dua fungsi f dan g dapat ditambahkan untuk menghasilkan sebuah fungsi baru f+g.

pandanglah fungsi-fungsi f dan g dengan rumus-rumus

Dari dua fungsi tersebut, kita dapat membuat sebuah fungsi baru f + g, yakni

Tentu saja kita harus sedikit hati-hati mengenai daerah asal. Jelas x harus berupa sebuah bilangan di mana f maupun g berlaku. Dengan kata lain, daerah asal f + g adalah irisan dari daerah asal f dan g (Gambar 1).

Gambar 1

Selain fungsi f + g, kita juga peroleh fungsi-fungsi baru yakni f-g, f.g, dan f/g. Dengan anggapan bahwa f dan g mempunyai daerah asal mula, kita peroleh sebagai berikut.

Kita harus mengecualikan 0 dari daerah asal f/g untuk menghindari pembagian oleh 0.

Kita juga boleh memangkatkan suatu fungsi. Dengan $f^n$, kita maksudkan fungsi yang memberikan nilai $\left[f\right(x){]}^n$ pada x. Jadi

Contoh:

Andaikan $F\left(x\right)=\sqrt[4]{4x+1}$ dan $G\left(x\right)=\sqrt{9-x^2}$, dengan masing-masing daerah asal natural [-1,∞) dan [-3,3]. Cari rumus untuk F+G, F-G, F⋅G ,F/G dan$F^5$ dan berikan daerah asal naturalnya (domain).

Penyelesaian: