Langsung ke konten utama

LIMIT FUNGSI TRIGONOMETRI

 Apa itu trigonometri?

Trigonometri merupakan cabang dari ilmu matematika yang mempelajari hubungan antara panjang dan sudut segitiga, biasanya digunakan dalam membuat desain bangunan, pembuatan jembatan, dan pada bidang astronomi.

DEFINISI
limit trigonometri merupakan nilai paling dekat dari suatu sudut. Istilah-istilah yang ada dalam trigonometri yaitu sinus (sin), cosinus (cos), tangen (tan), secan (sec), cosecan (csc), dan cotangent (ctg). Pada saat menentukan nilai dari suatu limitnya, beberapa cara/metode yang sering dipakai adalah substitusi, pemfaktoran, turunan, dan kali sekawan.

Turunan Trigonometri

f (x)f’(x)
sin xcos x
cos x– sin x
tan xsec2 x
cot x– csc2 x
sec xsec x tan x
csc x– csc x cot x

Artinya, limit x menuju a dari f(x) dibagi g(x) sama dengan limit x menuju a dari f(x) dibagi limit x menuju a dari g(x), asalkan syaratnya limit x menuju a dari g(x) tidak sama dengan 0. Karena, jika g(x) itu adalah 0, hasilnya akan tidak terdefinisi.

Sifat Limit Trigonometri

1. Limit Trigonometri - Rumus, Sifat, dan Contoh Soal - Materi Matematika Kelas 12 260

Sifat ini sama dengan sifat limit fungsi aljabar. Di sifat ini, limit x menuju a dari f(x) akan mempunyai nilai L atau akan sama dengan f(a) kalau f(a)-nya bukan.

2. Limit Trigonometri - Rumus, Sifat, dan Contoh Soal - Materi Matematika Kelas 12 262

Artinya, limit x menuju a dari f(x) kurang tambah g(x) sama dengan limit x menuju a dari f(x) kurang tambah limit x menuju a dari g(x).

3.Limit Trigonometri - Rumus, Sifat, dan Contoh Soal - Materi Matematika Kelas 12 263

Maksud dari sifat ini adalah limit x menuju a dari f(x) dikali g(x) nilainya akan sama dengan limit x menuju a dari f(x) dikali limit x menuju a dari g(x).

4. Limit Trigonometri - Rumus, Sifat, dan Contoh Soal - Materi Matematika Kelas 12 264

Artinya, limit x menuju a dari f(x) dibagi g(x) sama dengan limit x menuju a dari f(x) dibagi limit x menuju a dari g(x), asalkan syaratnya limit x menuju a dari g(x) tidak sama dengan 0. Karena, jika g(x) itu adalah 0, hasilnya akan tidak terdefinisi.

Batasan Fungsi Trigonometri

Dalam Matematika, limit fungsi diartikan sebagai pergerakan nilai fungsi mendekati batasan nilai tertentu yang paling mendekati nilai tersebut namun tidak pernah mencapai nilai tertentu tersebut secara tepat. Penulisan limit fungsi umum secara menggunakan notasi berikut:

Untuk membuktikan limit fungsi trigonometri maka digunakan Teorema Apit. Misal terdapat fungsi h, i, j yang terdefinisi pada interval terbuka L yang memuat a kecuali di a itu sendiri, sehingga berlaku fungsi h(x) ≤ i(x) ≤ j(x) untuk setiap x ϵ L dan x ke.

Sehingga berdasarkan Teorema Apit di atas terbukti bahwa nilai limit fungsi trigonometri berikut ini:

Sehingga kesimpulan teorema limit fungsi trigonometri untuk sembarang nilai real a, diperoleh:

Rumus Limit Fungsi Trigonometri 

Berikut ini rumus-rumus yang kerap digunakan: 

  • Limit sin x yakni saat x mendekati 0 adalah 0, rumus tersebut dapat dituliskan yakni sebagai berikut: lim sin x = 0, x -> 0 
  • Limit cos x yakni saat x mendekati 90 derajat adalah 0, rumus tersebut dapat dituliskan yakni sebagai berikut: lim cos x = 0, x -> 90 
  • Limit tan x yakni saat x mendekati 90 derajat adalah tak terhingga, rumus tersebut dapat dituliskan yakni sebagai berikut: lim tan x = ∞, x -> 90 
  • Limit cot x yakni saat x mendekati 0 derajat adalah tak terhingga, rumus tersebut dapat dituliskan yakni sebagai berikut: lim cot x = ∞, x -> 0 
  • Limit sec x yakni saat x mendekati 90 derajat adalah tak terhingga, rumus tersebut dapat dituliskan yakni sebagai berikut: lim sec x = ∞, x -> 90 
  • Limit csc x yakni saat x mendekati 0 derajat adalah tak terhingga, rumus tersebut dapat dituliskan yakni sebagai berikut: lim csc x = ∞, x -> 0 

Rumus limit fungsi trigonometri tersebut hanyalah berlaku untuk nilai x yang mendekati batas tertentu. Kemudian jika nilai x tidak mendekati batas tertentu, nilai limit pun dapat berbeda.

Contoh Soal Limit Trigonometri

  • Soal 1

Tentukan nilai limit fungsi trigonometri di bawah ini:

JAWAB: 

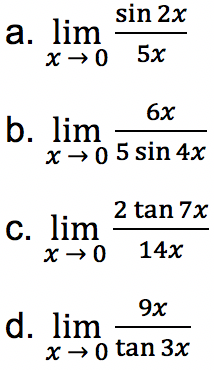
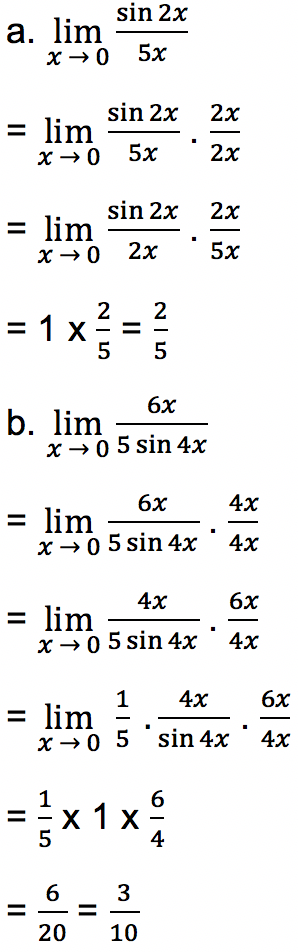
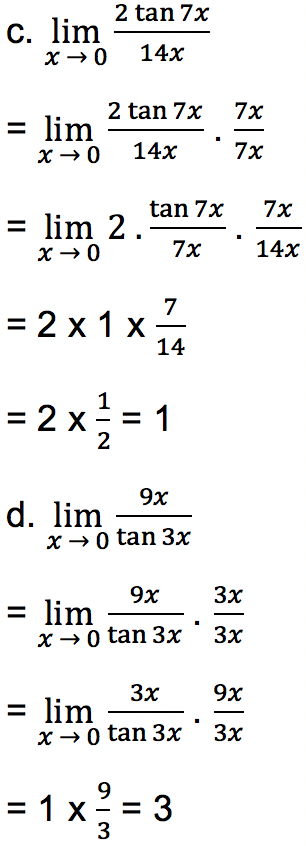
  • Soal 2

Terdapat sebuah fungsi campuran seperti di bawah ini:

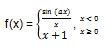
Contoh Soal Limit Trigonometri no 2 Bagian 1

Berapakah nilai a jika limit di x = 0?

JAWAB:

Untuk mengerjakan soal ini, kita harus memberlakukan batas limit kanan dan kiri.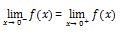Contoh Soal Limit Trigonometri no 2 Bagian 2

Uji nilai pada ruas kiri

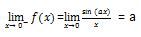
Contoh Soal Limit Trigonometri no 2 Bagian 3

Uji nilai pada ruas kanan

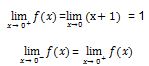
Contoh Soal Limit Trigonometri no 2 Bagian 4

a = 1

Untuk memenuhi persamaan di atas, maka nilai a=1






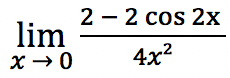
Komentar

Posting Komentar

Postingan populer dari blog ini

KEKONTINUAN FUNGSI

Berdasarkan Kamus Besar Bahasa Indonesia (KBBI), arti kata kontinu adalah berkesinambungan; berkelanjutan dan terus-menerus. Jadi maksud kontinu itu tidak terputus. Fungsi kontinu dalam matematika merupakan fungsi, yang jika di jelaskan secara intuitif, perubahan kecil dalam masukannya berakibat perubahan kecil pula pada keluaran.   DEFINISI KEKONTINUAN FUNGSI Fungsi f terdefinisi pada selang terbuka I yang memuat c . Fungsi f dikatakan kontinu di c jika limit  Kali ini kita akan mempelajari Penerapan Limit lainnya yaitu Penerapan Limit pada Kekontinuan Fungsi.  Fungsi f(x) dikatakan Kontinu pada suatu titik x = a  jika : f(a) ada  ada Jika paling kurang salah satu syarat diatas tidak dipenuhi maka f dikatakan Tidak Kontinu di x = a. Keterangan:   f(a) ada, maksudnya nilai fungsinya terdefinisi di x = a (bisa dihitung).  ada, maksudnya besar limit kiri dan limit kananya adalah sama. , maksudnya nilai limit dan fungsinya sama...
Posting Komentar
Baca selengkapnya

LIMIT FUNGSI BERNILAI REAL

Limit fungsi adalah sebuah konsep yang ada pada pelajaran matematika, limit biasanya digunakan untuk menerangkan suatu sifat dari suatu fungsi. Seperti halnya pada saat sebuah argumen hampir mendekati suatu titik tak terhingga atau juga sifat dari suatu barisan saat indeks hampir mendekati titik tak terhingga. Pada umumnya limit digunakan pada materi kalkulus dan juga cabang lain dari matematika yang berfungsi untuk mencari suatu turunan dan juga lanjutan. DEFINISI LIMIT S ecara umum limit didefinisikan jika f adalah fungsi yang telah didefinisikan oleh suatu interval terbuka dan mengandung a (dengan adanya kemungkinan pengecualian pada titik a) dan juga L merupakan bilang real.  Limit adalah suatu batas yang menggunakan konsep pendekatan fungsi . Jadi, bisa dibilang limit adalah nilai yang didekati fungsi saat suatu titik mendekati nilai tertentu. Dengan menggunakan  rumus matematika  di atas maka kita bisa membuat nilai f(x) menjadi sedekat mungkin dengan nilai L dengan...
Posting Komentar
Baca selengkapnya

KALKULUS DIFERENSIAL "Bilangan Real"

NAMA: GHEFIRA ARIQAH NASYWA NIM: 230101500017 KELAS: A11 PRODI: PENDIDIKAN MATEMATIKA ANGKATAN: 2023 Kalkulus diferensial adalah salah satu cabang kalkulus dalam matematika yang mempelajari bagaimana nilai suatu fungsi berubah menurut perubahan input nilainya. Nah,Mari kita mulai dengan BILANGAN REAL Bilangan real dapat dipandang sebagai label (penanda) untuk titik-titik di sepanjang sebuah garis mendatar untuk mengukur jarak ke kanan atau ke kiri (jarak berarah) dari suatu titik tetap yang disebut titik-asal (origin) dan diberi label  0. Bilangan real adalah semua bilangan baik rasional maupun irrasional. Namun kalian udah tahu belum,yang mana ya yang termasuk bilangan rasional? Bilangan Rasional  adalah bilangan yang dapat dinyatakan sebagai perbandingan dua bilangan bulat a dan b dengan syarat b tidak boleh sama dengan 0. Nah, bilangan rasional ini mencakup beberapa jenis bilangan didalamnya yaitu: BILANGAN ASLI (Natural...
Posting Komentar
Baca selengkapnya